Explorations among Happy Numbers

I’ve recently been watching through a bunch of old Numberphile videos. Several of them feature sequences generated by manipulating the digits of a numbers. Invariably, these numbers are represented in decimal, leaving me curious about about how such sequences behave in other bases. My first question: what about happy numbers? Here’s a quick rundown of what happy numbers are:

I wrote a few Python functions to quickly check different numbers in different bases. As a nod to the Babylonians, I considered every base up to 60, checking every number less than 10,000 and counting how many of them were happy. Here are the results:

0: 0
1: 0
2: 9999
3: 1988
4: 9999
5: 2571
6: 645
7: 162
8: 549
9: 627
10: 1441
11: 196
12: 24
13: 582
14: 93
15: 164
16: 2585
17: 253
18: 4154
19: 3647
20: 1616
21: 45
22: 17
23: 19
24: 9
25: 519
26: 377
27: 279
28: 6
29: 1730
30: 5265
31: 11
32: 11
33: 84
34: 192
35: 77
36: 50
37: 58
38: 18
39: 26
40: 139
41: 850
42: 66
43: 10
44: 5
45: 58
46: 59
47: 5
48: 4
49: 9
50: 42
51: 48
52: 31
53: 62
54: 10
55: 106
56: 5
57: 5
58: 61
59: 33
60: 27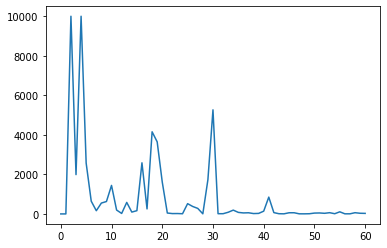

A few things that jump out:

• All natural numbers are happy in base 2 and base 4. It’s clear why this should be the case in base 2 - the only digits you ever come across are 1 and 0; it’s not immediately apparent why it’s also true for 4.
• There’s a general trend that, as the base rises, a smaller proportion of numbers are happy. But it’s not at all linear - there are many happy-number-rich bases surrounded by happy-number-poor bases, and vice versa. Among these:
  • bases in the 16-20 are relatively happy-number-rich
  • there’s an isolated peak at base 41
  • what’s going on with base 30? In both base 28 and 31, about 0.1% of all numbers are happy. But in base 30, more than half of them are. Why?
  • base 48 features the smallest proportion of happy numbers among the bases I checked. It may have something to do with 48 having many factors of 2 and 3—base 12, base 24 and base 32 are also local low points—but this can’t be the whole picture: base 6 and base 9 are hardly local minima, base 31 (prime) is just as happy-number-poor as 32, and base 16 is a local maximum.

This investigation has only scratched the surface, and I hope to keep exploring the topic. Some questions that I’m curious about:

• Are happy numbers evenly distributed as we look at larger numbers, or does the distribution trail off?
• A number is unhappy if its sequence gets stuck in a loop. How long do cycle lengths get? Do cycle lengths tend do be longer for larger numbers? Do some bases tend to have sequences with longer cycles?

If you’re interested in looking at this in more detail, here’s a full list of all happy numbers up to 9,999 in bases up to 16 along with their representation in those bases, happy numbers up to 99,999 in several happy-number-poor bases, and happy numbers up to 999,999 in base 48. The code, including general functions for converting numbers between different bases, functions for searching for happy numbers, and the jupyter notebook in which I did my calculations, is on github.